我われは、熱平衡にある気体の温度が一定していることを日常的に実感しています。熱力学では状態によって決まる物理量として内部エネルギーUが登場し、気体分子運動論に基づいてU=3NkT/2という関係式が導かれます。マクロの観点からは、Tが定まっておればUも定まるはずです。しかし、統計力学ではミクロの気体分子の運動状態に対して確率論を使って系のエネルギー(マクロの物理量Uに相当)を計算するので、期待値からのずれ(Uのゆらぎ)を扱うことが可能です。この考察によって、Uが事実上一定値をとるという結論になることを、参考資料に挙げた書物で勉強しました。この記事はその備忘録です。
1.F=U-TSから状態和Zの導出
ヘルムホルツの自由エネルギーの定義式F=U-TSとボルツマン原理の式S=klogWとから, 多粒子系の状態和Zを導くことができる。
によって関係づけられる注[i])。 (1)と(2)を対比する
となる。多粒子系の状態和は、第2節で出てくるカノニカル分布の式(8)の分母をさし、
と定義される。ここで、Ej(j=1,2,…)はカノニカル分布をとる粒子系の微視的状態のエネルギー、Gjはその微視的状態の数である。状態和Zは系のとるすべての微視的状態についてGj e- Ej/kTの和をとったものであるが、(3)は系のエネルギーEj=U、微視的状態数Gj=Wの項のみでZが表されることを示している。このことは、統計力学の観点から多粒子系のエネルギーが一定値Uに定まることを暗示している。
2.カノニカル分布
マクロの系の内部エネルギーが上記のように一定値に定まることを議論するには、気体分子集団の運動エネルギーの分布を知らねばならない。このためにカノニカル分布を使うので、この説明から入る。
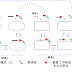
粒子系(系A)が大きい熱浴(系B)に接していて、両者の間では熱の出入りが可能で、温度が一定値Tに保たれているとする。さらに、系Aと系Bを合わせた全体の系ABは孤立系であるとする。Γ空間にエネルギーEjの微視的状態が入り、その数をGjとする。このような状況下にある微視的状態jが現れる確率を求めよう。
孤立系の微視的状態はすべて等確率で実現されるので、総エネルギーがEABの系ABがとる微視的状態数WAB(EAB)は、
と表わされる。ここで、WB(
となる。熱浴系Bのエントロピーはボルツマンの原理によって
で与えられる。系Aのエネルギーは
ただし体積一定として、微分を用いた。2次の項以下を無視して
となる。(6) と (7)から
これを(5)へ代入して
だから
となる。これがカノニカル分布の式で、エネルギーEjの微視的状態の出現確率を表す。
3. 気体分子集団の運動エネルギー
これからアプローチするマクロの系は、「体積Vの空間を飛び回るN個の理想気体分子であり、温度Tで熱平衡状態にある」とする。この場合に、あるエネルギーをもつ多粒子系の微視的状態の出現確率を求めるのが、目下の課題である。
と表わすことができる。これら二つの関係によって(8)の分母(粒子系の状態和Z)は、
各々の分子i (i=1,2,…)に対して、位置空間の定義域V(体積Vと区別して赤字)での積分は
と求まるから
となる。
とする。
(8)を連続型の表現に変換すると、Ej、Gj、Pjは、Γ空間の座標(q1, q2, …q3N, p1, p2, …p3N)で決まる変数E、G、Pになり、(9)により(8)は、
に変換される。気体分子からなる系では、エネルギーが位置座標によらないので、この式の両辺を位置空間の定義域で積分すると各辺でVNが出て相殺され、上の式は運動量空間で定義された式
に書き変わる。
ところで、(10)のP (p1, p2, ,…p3N)は、系のエネルギーEにおける微視的状態の確率密度関数P(E )を表すので、P(E )dEは系のエネルギーがE~E +dEにあるときの確率密度、すなわち微視的状態の出現確率で
と表わすことができる。G(E )dEは、系のエネルギーがE~E +dEにあるときの微視的状態数であり、G(E )はエネルギーEにおける微視的状態の密度を表し、状態密度と称せられる。
いま、エネルギーEの等エネルギー面で囲まれた位相空間の領域を考え、その領域内の微視的状態数をN(E)とする。エネルギーがEからE +dEに変化すると、この変化に伴うN(E)の変化数dN(E)は、変化の前後の等エネルギー面の間を占める領域の微視的状態数、すなわち系のエネルギーがE~E +dEにある微視的状態の数G(E ) dEに等しい。したがって
と表わされる。
次にG(E )を求めるためにN(E)の計算をする。 そもそも、粒子系のとる微視的状態の数は、Γ空間の定義域の体積を細胞の体積ɑNで割ることによって求められる。よって、エネルギーがE以下(Ej≦E)である系の微視的状態の数N(E)は、
である。なお、同じ空間を飛び回るN個の気体分子は互いに入れ替わっても、微視的状態が変わらないのでN !で除した。右辺の積分は半径p=(2mε)1/2の3N次元の球の体積で、計算の結果となる注[iii])。よって、(12)により系のエネルギーがEのときとなる。この式を(11)に代入して、系のエネルギーがE~E +dEにあるときの一つの微視的状態の出現確率はと計算される。そしてEの確率密度関数がと表わされ、0≦E<∞の区間で積分すれば1となる注[iv])。Eの増加とともに、Nが非常に大きいと
の解で与えられる。カギ括弧をゼロとおきこれは内部エネルギーUの式に他ならない。
3.エネルギーのゆらぎの計算
次にこのエネルギーの分布を確率の観点から見てみよう。このためカノニカル分布に従う多粒子系のエネルギーのゆらぎを定式化する。多粒子系の微視的状態に番号をふり、n番目の微視的状態のエネルギーをE(n)とする。系のエネルギーの平均値(期待値)EからのE(n)の偏差、すなわちエネルギーのゆらぎは、(E(n)-E )2の平均の平方根として定義される。<E(n)>=E であるから
<(E(n)-E )2> = <(E(n)2-2 E(n)E +E 2)>
= < E(n)2>-E 2 (14)
と書き替えられる。カノニカル分布において、一つの粒子系がエネルギーEjの微視的状態をとる確率Pjは
で与えられる((8)で1/kT=βとおいて書き換えた)。したがって系のエネルギーの平均値は
となる。右辺を書き直して
この変形で、Ej(j=1,2,…)が一定のとき体積が一定であることに留意した。また、E(n)2の平均<E(n)2>は、E(n)=Ejとおいて
となる。したがって、エネルギーのゆらぎは、(14)の右辺に(16)と(14)を代入しと求まる。β=1/kTの微分は、dβ=(-1/kT2)dTだから
この変形で(16)を用いた。ところで、(∂E/∂T)Vは粒子系の定積熱容量であり、これをCvとおくと、エネルギーのゆらぎは
と表わされる。
ここでゆらぎの大きさを見積もってみる。定積熱容量の定義からV一定なら
零点エネルギーを無視すればE=TCvである。また、粒子数をNとするとE=3NkT/2でありkT=(2/3)E/Nだから
となる。カノニカル分布の微視的状態数は大きいので、E(n)は中心極限定理によって平均値がEで、標準偏差σが
参考資料
1.杉田元宣 著「熱力学及び分子統計論」南江堂1957、pp. 82-86 (§20 状態和と状態数)
2.https://ocw.kyotou.ac.jp/wpcontent/uploads/2010/04/2010_toukeibutsurigaku_2.pdf富田博之「『統計物理学』講義ノート」、2005 年3月4版、pp. 37-39(§4.1 カノニカル分布)
3.都築卓司 著「統計力学入門 自然科学になぜ統計が必要か」総合科学出版、1969、pp.92-101(§2.5状態密度)
4.藤原 邦男 , 兵頭 俊夫 著「熱学入門 マクロからミクロへ」東京大学出版会 1995、 pp. 110-136(第7章 統計力学の方法)、 pp. 137-159 (第8章 熱的ゆらぎ・エントロピー)
5.和達 三樹 , ⼗河 清 , 出⼝ 哲⽣ 著「ゼロからの熱力学と統計力学」岩波書店2005、 pp. 93-150(第5章 古典統計力学、第6章 正準集団)
6.桂 重俊, 井上 真 著「統計力学演習」東京電機大学出版局 1993、pp. 41-69(第3章 ミクロカノニカル集合の方法)、pp. 2576-257(付録A 数学的補遺)
7.戸田 盛和 著 「統計力学概論」朝倉書店1952、pp. 183-184 (§49エネルギーのゆらぎ)
(後記)
第1節は、参考資料1を参考にした。本文の式(1)~(3)の計算はこの資料による。
第2節は、参考資料2の解説に沿って敷衍説明した。
第3節は、参考資料3~5を参考にした。
第4節は、参考資料4、5、7を参考にした。
予め知人に原稿のレビューを依頼しました。その折のコメントや提案を取り入れて本記事を完成しました。
無断転載禁止
注[i])
ヘルムホルツの自由エネルギーFを一粒子の状態和zと関係づける式(F=-NkTlogz)は、前回のブログ「統計力学に出てくる未定乗数βの熱力学的意味(2)」において導出した。多数(N個)の粒子から成る系の状態和Zは、個々の粒子の状態和zとの間に、Z = zNの関係があるので、(2)で表される。


















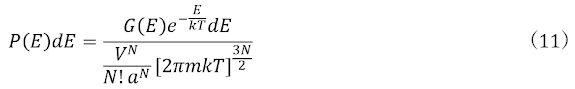










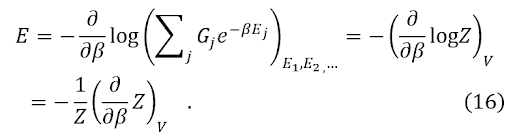











0 件のコメント:
コメントを投稿