理想気体の状態方程式が出てこない熱・統計力学を考えてみました。マクロの現象として固体比熱のデュロン-プチの法則があります。この法則はミクロの観点から固体比熱にアプローチする統計力学によって説明されます。そもそも、統計力学ではボルツマン分布を導出する過程で、ラグランジュの未定乗数法が使われます。そのとき使う未定乗数βとして、気体の分子運動の力学に基づいて得られた関係式
β=1/kBT (kBはボルツマン定数) が一般的に用いられます。「ガスぬき」の熱・統計力学ではこのようにせず、βを金属の単原子結晶のモル熱容量と結び付けた関係式を導いてみました。
1.熱力学の観点から
話題とするのは、「ガスぬき」の熱力学だから固体が対象です。固体比熱のデュロン-プチの法則に従うような金属の単原子結晶をとりあげます。
この法則によれば、その熱容量は金属の種類によらず、モル熱容量が3R (= 8.3145 J mol-1K-1)と一定の値になる。モル熱容量が金属の種類によらず、モル数つまり原子数によって決まる点は、理想気体の状態方程式(pV=nRT)によると、気体の種類によらず、ある温度のpVで表されるエネルギーがモル数nによって決まるのと類似する。常温付近の単原子結晶のモル熱容量をCm 、アボガドロ数をNAとすると、N 個の原子からなる結晶に対して内部エネルギーと温度のそれぞれの変化量の間で次式が成り立つ。
ここで、積分定数U0はT=0での内部エネルギーである。
2.統計力学の観点から
固体の内部エネルギーをミクロの粒子の運動と関係づけるために、固体比熱のアインシュタイン模型の復習から始めます。
この模型では、N個の粒子がすべて同じ振動数(ν)でそれぞれ独立に振動しており、振動子のエネルギーの総和 (E)が一定であると考える。まず、一個の粒子の1次元の振動について説明する。量子力学によると、最低レベルからn番目の振動子のエネルギーは、プランクの定数をh、振動子の振動数をνとすると
である。N個の振動子を、エネルギーε0の状態にn0個、ε1の状態にn1個、……εiの状態にni個、……になるように分布させるとする。この分布{n0、n1、…… ni、……}をとるように振動子を配置する仕方の数は
である。アインシュタイン模型では、振動子の総数Nと全振動子のエネルギーの和Eがそれぞれ一定であるので、
と表わされる。
となる。
一方、状態和(6)の対数をとると
だから、logZをβで偏微分して
したがって、この式と(7)とから
ここまでは1次元の調和振動子の計算であったので、3次元の調和振動子のエネルギーE3Dは、3方向の振動が独立しているとすれば、上式の3倍で与えられる。
これは振動子N個の系のエネルギーで、熱力学の内部エネルギーに当たる。したがって、
3.まとめ
統計力学で導かれた式(9)を熱力学の内部エネルギーの式(1)と比較すると、右辺の第1項は振動子の零点エネルギー U0 、第2項は温度に関係するエネルギー (N/NA)CmT に対応している。hνβ ≪1 の場合には、exp(hνβ) = 1 + hνβ だから
この式と(1)との対応から
となって、内部エネルギーと温度の関係式が得られる。
この式はN個の原子からなる結晶の内部エネルギーを表すので、これをTで偏微分すれば熱容量が得られ、1モル(N =NA)の熱容量は ∂U3D/∂T = Cmとなる。
また、(10)から次のことが明らかになる。(Cm/NA)Tは内部エネルギーU3Dのうち温度に関係する部分であり、(10)の右辺はCmTをNAで割った値だから、調和振動する原子1個が持っているエネルギーに当たる。ここで κ = Cm/NA とおくと
となる。「理想単原子結晶」に対して「熱容量定数κ」なるものを想定すれば、理想気体の熱力学における気体定数 R の役割をこの定数にもたせることができよう。
ところで、(9)に続く計算ところで、hνβ ≪1という条件を使った。この条件は(10)によってhν ≪ (Cm/3NA)Tであって、1 個の振動子が零点エネルギー hν/2 より十分大きなエネルギーで振動する場合、すなわち高温であれば実現する。このとき(9)の温度が関係する項がhを含まない式に変換されるのは、量子力学から古典力学への移行に対応している。
最後に、κ とボルツマン定数 kB との関係をみてみます。気体の運動に着目する一般の統計力学では、熱平衡にある気体分子の自由運動の力学に基づいて、
が導かれる。このβを(10)に代入するととなって、κ = 3kBである。また、この関係から
となり、デュロン-プチの法則を表す式が得られる。
参考資料
1.
原島 鮮著「熱力学 統計力学」培風館、1966
2.
中村 伝著「統計力学」岩波書店、1967
3. 砂川重信著「エネルギーの物理学:現代物理学入門」河出書房新社、1972
4.小出昭一郎著『物理学 三訂版』(三訂第57版)裳華房、2008.
5.
P.
Atkins, J. de Paula著、千原秀昭、中村亘男訳「アトキンス 物理化学(下) 第8版」東京化学同人、2009
6. 都築卓司著「新装版 なっとくする量子力学」講談社、2018
注1)この導出は、成書にゆだね、物理学については門外漢の私が、ボルツマン分布を理解するのに役立ったYouTubeのサイトを紹介しておきます。https://www.youtube.com/watch?v=YelovOPe5mM&t=41s です。また、その導出の際に使うラグランジュの未定乗数法はインターネットのサイトhttps://www.yunabe.jp/docs/lagrange_multiplier.html で勉強しました。
後記
物理学については門外漢ですが、若かりし頃に酵素反応のメカニズムに興味を持ったこともあって、物理化学を勉強する機会がありました。その折に、量子力学や統計力学を少しかじった経験があります。隠居暮らしを始めてから暇に飽かせて統計力学に再挑戦しています。今回の記事はその産物です。一緒に考えてもらえる知人の協力があって、この記事を完成することができました。
無断転載禁止






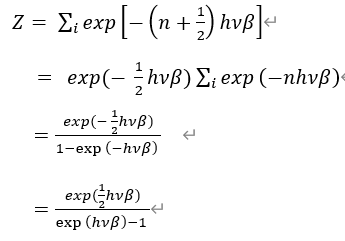







0 件のコメント:
コメントを投稿