ある知人が、ときに国際宇宙ステーションの観測日時を知らせてきます。デジカメで撮影を試みたり、人工衛星の円運動の力学を勉強したりしてみました。これだけやれば、「ボーと見てんじゃねーよ」とチコちゃんにしかられずにすみそうだと自画自賛です。物理学の教科書には、等速円運動する物体が受ける向心力の加速度は、速度の2乗を半径で割った商に等しいと書かれています。ニュートンはこの関係をどのように導き出したかを知ろうと調べてみました。今回は、そのまとめです。ニュートンによる等速円運動の加速度の導出には、内接正多角形の辺に沿った運動や円運動からそれた物体の落下運動が使われました。ニュートン流の導出をたどってみます。現代の力学書にある標準的な方法にも触れます。最後に、上記の等速円運動の加速度を使って、太陽が惑星に及ぼす引力が、軌道半径の2乗に反比例することを示します。初めに、参考にした資料を掲げておきます。
1)中島秀⼈著『ニュートンに消された男 ロバート・フック』(角川ソフィア文庫)、2019
2)アイザック・ニュートン著、中野猿人訳・注『プリンシピア 自然哲学の数学的原理』講談社、1977
3)山本義隆著『原子・原子核・原子力―私が講義で伝えたかったこと』岩波書店、2015
4)エス・イ・ヴァヴィロフ著、三田博雄訳『アイザック・ニュートン』東京図書、1958
5)和田純夫著『プリンピキアを読む』講談社、2009
6)小出昭一郎著『物理学 三訂版』裳華房、2008
7)高橋義郎著『力学の発見―ガリレオ・ケプラー・ニュウートン』(岩波ジュニア新書)、2013
ニュートンが最初に等速円運動の向心力の導出を試みたときのアイデアの話から始めます。参考資料1に、ニュートンが等速円運動の遠⼼⼒を導くのに、図1のように物体が円形の壁にぶつかって跳ね返るモデルを使ったことが載っています。彼はペストの流⾏を逃れて帰郷した折(1666年)に、いろいろな研究のアイデアを「雑記帳」に記しましたが、その中に書かれているそうです。ニュートンは、物体が正多⾓形の辺に沿って進み、各頂点で外接円によって反射されるような運動を考えました。このモデルは、時を経て1687年に出版されたニュートンの主著『プリンキピア』の第1編1章命題4の説明の最後(参考資料2)にも出てきます。その部分の要旨は次のようです。
物体が反射するとき円に突き当たる力は、その速度に比例するはずである。また、物体が一定時間当たり円に及ぼす力の総和は、その速度と反射回数との積に比例すると考えることができる。一定時間当たりの反射回数は速度注1に比例し、円の半径に反比例する注2ので、物体が円に及ぼす力の総和は、その速度の2乗を半径で割った商に比例することになる。そして、多角形はその辺を無限に小さくすると円に収束するので、円運動においても同じ関係が成り立つ。物体が円に及ぼす力が遠心力で、この力と逆向きで大きさが等しい向心力が物体を中心へ向けて押し返す。
―――――――――
注1参考資料2には、「与えられた時間内に描く長さ」と書かれているので、「速度」と表現しました。
注2多角形がそのまま大きくなれば、一定時間当たりの反射回数は多角
物体が円形の壁によって反射される現象に現代風にアプローチします。参考資料3(56-57頁)の気体分子運動論の解説に、その答えがありました。気体分子が球形の容器に入っていて、壁面と弾性衝突を繰り返す運動によって分子が器壁から受ける力が計算されています。一個の分子の運動を考えます。衝突は極短時間Δtで起き、そのときだけ分子は力fを受けるので、相次ぐ衝突の時間間隔tの間に物体が受ける力の加重平均<f>は、fがその間一定と近似すれば、次の式で表されます注[i])。
―――――――――
注1参考資料2には、「与えられた時間内に描く長さ」と書かれているので、「速度」と表現しました。
注2多角形がそのまま大きくなれば、一定時間当たりの反射回数は多角
<f>={f×Δt + 0×(t-Δt)}/t = fΔt/t
 |
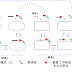
| 図1.正多角形の辺に沿った運動。正8角形の辺の頂点でその外接円の壁によって反射される様子を示す。反射の際の力積から、物体が円の中心に向かって受ける力を計算することができる。ニュートンが描いた図は、正方形の辺に沿った運動で、参考資料1の275頁にある。 |
図1のように、質量mの分子が速度vでA→Bと進んでBで反射し、B→Cと進むとします。このとき分子の運動量mvのBOに直角方向の成分は変わりませんが、∠ABO =∠CBO =θとすると、BO方向の成分には2mv cosθの変化が起きます。運動量の変化量は分子が受ける力積に等しいので、fΔt=2mv cosθです。また、ABの距離は、球の半径をrとすると2r cosθで、この距離を分子が移動する時間はt=(2r cosθ)/vとなるので、
<f>=fΔt/t = 2mv cosθ/{(2r cosθ)/v} = m(v2/r)
です。したがって、分子に作用する加速度の時間平均はv2/rになります。この結果は多角形の辺の数に依存しません。分子を物体に置き替えれば、物体の円形の壁による反射がもたらす向心力の加速度が求められます。多角形の辺の数が多くなると円に収束するので、円運動においても加速度は、v2/rになります。ここで、fΔtは衝突による力積の近似表現です。詳しくは注[i]を参照して下さい。
このように円形の壁による反射を解析的に扱うと向心力の加速度が求まりますが、ニュートンが上記の正多角形の辺に沿う回転運動のモデルから求めたのは遠心力で、これと釣り合う力として向心力を考えました。のちに、ニュートンは慣性運動する物体が円の中心に向かって絶えず落下しているのが等速円運動だと考えて、その加速度を導出しました。ただし、このアイデアは、R.フックによる惑星の運動についての見解がヒントになったようです。彼は、1679年にニュートンに手紙を送り「惑星の運動を接線に沿う直線運動と中心の物体に向かう吸引運動との複合とみる」という見解について意見を乞いました。これがきっかけとなって、ニュートンが力学の問題に本格的に取り組むようになったと見られています(参考資料1、293-295頁、参考資料4、131-132頁)。
では、ニュートンはどのように円運動の加速度を導出したのでしょうか。その筋道をたどってみます。その先に万有引力が見えてきます。
参考資料5(125-127頁)にある解説を参考にしました。図2に示すように、左回りに円運動をしている物体が円周上の点Aで円運動から極短時間それて接線方向のCに達したあと、Cから直径AGに平行に移動して円周上の点Bに至るとします。これは円運動によるAからBへの変位を慣性運動と落下の二つの運動に置き換え、それらを近似したものですが、後に厳密に扱います。
まず、移動距離BCを幾何学で求めます。BDはBから直径AGに下した垂線です。△ABCと△GABは相似な直角三角形(∵ ∠BACと∠BGAは、∠BADと足すと90度なので、等しい)であるから、AB/BC = GA/ABであり、ゆえにBC = AB2/GAとなります。BをAに近づけた極限で、弧AB=ABになるので、
BC = 弧AB2/GA
です。
ここで、AからBに短時間進む等速円運動を考えます。この運動によってAにおける接線上の点C(∠ACB=90°)からBへの縦方向の変位が生じます。この変位は円軌道からそれた物体が元の軌道へ戻るイメージから落下とみることができます。この落下をもたらすのは円運動の向心力と考えます。この向心力は実際には物体がAからBに進む間、物体に作用したものですが、それがAからCに進む慣性運動の間はお預けになり、落下のときに作用すると考えます。これは上で円弧AB間の運動を二つの運動に置き換えた後者に対応します。この向心力による加速度ベクトルαの大きさα=|α|は円軌道上で一定で、方向も微小時間においてはほぼ一定なので、ここでは加速度は一定とみなすことにします。するとCからBへの運動はガリレオの落下の法則に従います。円運動をしている物体が慣性によりCに向かう直線運動から外れていくのを向心力による落下とみているのですが、ACは接線なので落下の初速度はゼロです。物体が等速円運動によりAからBに進む微小な時間をtとすると落下時間もtに等しく、落下距離BCは落下の法則により
BC=αt2/2
です。上記の幾何学の関係は、円の半径をrとして
BC = 弧AB2/2r
だから、
αt2/2 = 弧AB2/2r ∴α=(弧AB/t)2/r
弧ABは物体の移動距離だから、弧AB/tは速さです。速さをvとすると、
α=v2/r (1)
が得られます。
以上、ニュートンが円運動の向心力の導出に至った経緯をたどりました。ここで、現在の標準的な方法で円運動の力学を厳密に扱ってみます。速度、加速度の力学的概念が数学的に確立され、微積分など数学的手段も整備された現在、それらをほとんど機械的に扱うことができます。まず、物理学の教科書(参考資料6,7-9頁)に載っている予備知識から始めます。
物体がxy平面上で半径rの円周上を一定の角速度ωで回転する運動は、位置ベクトルrのx成分とy成分で表されます。
x = r cosωt, y = r sinωt
これらをtで微分して、速度ベクトルvのx成分とy成分
vx = -rω sinωt,
vy = rω cosωt
が得られ、さらにtで微分して、加速度ベクトルαのx成分とy成分は
αx = -rω2 cosωt = -ω2x,
αy = -rω2 sinωt = -ω2y
となります。ゆえに、α = -ω2rとなり、加速度は円の中心に向かいます。その大きさは半径のω2倍です。
 |
円運動をこのように表して、図2で示したような接線方向にそれる運動と接線上からの落下を解析しやすくするために、図2を右へ90度回転します。GAがx軸に一致し、これに垂直で中心Oを通る直線がy軸になります。Oが座標の原点です。円運動において、t=0でA(r,0)にあった物体は時間tの後に円周上のB(r cosωt, r sinωt)に移動します。この運動を二つに分けます。まずAから慣性により弧ABと等しい距離を進んでC’(r, rωt)に至る運動Maが起き、それにC’から加速度を受けてBに達する運動Mbが続くとします注[ii])。図2におけるCも図3に印しました。CはBからAC’に降ろした垂線の足で、直線運動の速度を円運動と同じ速度rωとすると、Aからの到達時間はtよりも短くなります。しかし、その差はt3のオーダーで注[iii])、tが小さい場合の近似計算においては無視できる可能性があります。したがって、図2は落下の状況を見やすく描いた近似図と言えます。
さて、図3に示したA→C’→Bの運動を解析的に扱ってみます。運動の始点から終点に至る変位ベクトルは、運動Maでは(0, rωt)で、運動Mbでは(r cosωt-r, r sinωt-rωt)で表されます。これらの変位ベクトルの成分をtで微分すれば、それぞれの運動の速度ベクトル(0,
rω)と(-rωsinωt,
rωcosωt-rω)が得られ、速度ベクトルをさらにtで微分すると、それぞれの運動における加速度ベクトル(0, 0)と(-rω2 cosωt, -rω2
sinωt)が求められます。
tが十分小さければ、3角関数の級数展開の最初2項を使って近似できるので、運動Mbについて、近似的に変位ベクトルは(-rω2t2/2, rω3t3/6)と表わされ、速度ベクトルは(-rω2t,
-rω3t2/2), 加速度ベクトルは(-rω2, rω3t)となります。これらのベクトルで、y成分はx成分よりtの次数が1オーダー大きいので、y成分を無視すると、それぞれ(-rω2t2/2, 0)、(-rω2t, 0)、(-rω2, 0)になります。加速度ベクトルに注目すると、運動Mbは、x軸に沿った、加速度の大きさがrω2の落下運動であることが分かります。この状況を描いたものが図2になります。また、変位ベクトルから、落下距離がrω2t2/2 = αt2/2となって、落下の法則と一致します。落下速度はrω2t = αtです。円運動をしてる物体の速度をvとするとv = rωであり、加速度はα = rω2=(rω)2/r=v2/rとなって式(1)と同じになります。
ここで、ニュートンの時代に問題であった太陽をめぐる惑星の運動に話を移します。惑星の運動が等速円運動と仮定して話を進めます。太陽が惑星に及ぼす引力は、惑星に加わる向心力に等しく、容易に計算することができます(参考資料7、143-144頁)。
惑星の質量をmとすると向心力の大きさはf = mv2/rで、惑星の公転周期をTとするとv=2πr/Tで表されるから、
f = m×4π2r/T2
(2)
となります。ケプラーの第3法則によれば、円軌道の半径と惑星の公転周期との間にはr3/T2=定数の関係があるので、
f = 4π2rm/T2=4π2m×定数/r2 (3)
ここで、式(2)を月の運動に適用してみます。軌道半径r=3.84×108m(=38.4万km)、公転周期T=2.36×106秒(=27.3日)を式(2)に代入すると、月の受ける向心力は月の質量をM ㎏として、M×2.71×10-3m・㎏/s2となります。また、仮に月と同じ質量の質点を地上に置くと、重力加速度が9.81m/s2であるから、地球の引力が‘地上の月’に及ぼす力はM×9.81m・㎏/s2です。この力の大きさは、実際の月が受ける向心力の約3620倍です。ところで、惑星の運動から明らかになった式(3)の関係が、月の運動でも成り立つとすれば、地球が月に及ぼす引力は、円軌道の半径の2乗に反比例するはずです。地球の中心注[iv])から月までの平均距離は地球の半径の約60.3倍なので、月に及ぶ引力は地上の1/60.32≒1/3640となります。上の計算のように月が受ける向心力が‘地上の月’に働く引力の1/3620で、二つの計算値がうまく一致することが分かります。
ニュートンが地球の引力が月に及んでいることを証明した方法は上記と少し違いますが、本質的に同じです。図2に示すような月の落下を考え、一定時間の落下距離(天空での)から逆2乗則によって上記の仮想的な‘地上の月’の落下距離を求め、この距離が地上の物体の落下距離に等しくなることを示しました。説明の詳細は、参考資料5(52-56頁)に載っています。このようにして、ニュートンは、引力が太陽と惑星の間だけでなく、地球と月の間でも働いていること、さらに、月の落下と地上における物体の落下が同じ地球の引力に基づくことを明らかにしました。そして、あらゆる物の間で逆2乗則に従う引力が働くというアイデアから万有引力の仮説を打ち立てました。
注[i])力fが加わると物体の運動量 p = mvは変化する。その変化量 P= Δp = m(v2-v1)を力積と呼ぶ。Δtの間作用した力fの力積は積分P = ∫0Δtf(t)dtであるが、瞬時に終わる衝突などにおいては、前後の運動量の差として扱った方が便利である。
全時間tのうちの最初のΔtの間はf ≠ 0、それ以外でf =
0なら、力fの全時間平均は
<f>= {∫0Δtf(t)dt +∫Δttf(t)dt}/t = ∫0Δtf(t)dt/t = P/t
である。Δtの間、fが一定でそれ以外でf=0なら、上式は
<f>= {f×Δt+0×(t-Δt)}/t = fΔt/t = P/t
と簡略化される。ここではfΔtが力積である。衝突のようにΔtを無限小とみなす場合、fの全時間平均は、両式において力積Pを一定に保ちながらΔt→0とした場合の極限で、極限においても<f>= P/tは満たされる。
注[ii]) これら二つの運動が逐次的に進行すると、円運動の場合の2倍の時間を要する。円形鋸歯状の回転で一周に円運動の2倍(2π/ω)×2)の時間がかかるのは、円運動では同時に併行して進行する二つの過程を分けたので当然である。
注[iii]) AC’= rωt、AC = DB = OB sinωt = r sinωt ∴CC’ = AC‘-AC = r (ωt-sinωt)。sinωt =
ωt-(ωt)3/3!
+ ‥‥と級数展開されるので、CC’ = (ωt)3/3!
+ ‥‥となる。AC方向の運動は等速だから、時間の差は距離の差CC’に比例するので、時間tに対してt3のオーダーである。
注[iv])地球の引力について、質量がその中心に集中しているとして逆2乗則を使うことができるのは、球形の物体(密度分布が球対称)による引力は、外部においてはその質量が中心に集まった場合と同じだからである。
(追記)一緒に考えてもらえる知人の協力もあって、この小文を書き上げることができました。
なお、この知人から「人工衛星の高度と周回の周期の関係に触れるのはいかがですか。」というコメントがあり、次のようにまとめてみました。
地上400 kmの高度で周回する国際宇宙ステーションの公転周期 T(秒)を計算してみます。r3/T2 =常数(ケプラーの第3法則)の関係は、月の軌道にも、人工衛星の軌道にも適用できます。月の軌道半径r=3.84×108m(=38.4万km)、公転周期T=2.36×106秒(=27.3日)で、地球の半径は6.37×106mだから、次の等式が成り立ちます。
(3.84×108) 3/(2.36×106)
2 = ((6.37+0.4)×106) 3/T2
∴ T2 = {(6.37+0.40)×106} 3×(2.36×106)
2/(3.84×108) 3
=(6.773×2.36 2/3.84
3)×(1018×1012/1024) =30.52×106
T = 5.524×103秒= 92.076分となります。