大学の同期生の会(平成30年3月31日開催)の世話人から「水素をH2、酸素をO2、水 をH2Oと表し、水素と酸素の反応を『2H2 + O2 → 2H2O』と表すようになった経緯」を語って欲しいとの依頼がありました。「原子説・分子説」が確立した歴史をたどれば分かるはずと思い、化学史関連の本も数冊持っていたので、読んでみる良い機会と考えて引き受けました。この小文は、その時作ったスライド原稿をもとにまとめたものです。
I 原子説・分子説の確立
① 近代的な原子説の確立以前の状況
ルネッサンスによって、古代ギリシャの原子説が復活し、 17世紀には、粒子的物質観を持ったボイル(1627-1691)やニュートン(1642-1727)のような物理学者が登場した。化学の分野では、ドルトンが近代的な原子説を提唱する前の18世紀後半に、酸素、窒素、水素などの元素や炭酸ガスのような化合物が続々と発見され、ラボアジェが近代化学の基礎を固め、「化学要論」(1789年)を著した。その中で、化学分解できない物質を元素と定義し、歴史上初めての元素表を示した。
②近代的な原子説の確立
1808年に、ドルトン(イギリス)が化合物を構成する原子について考察し、著書「化学の新体系」の中で原子説を説いた。次の二点が今日に受け継がれているキーポイントである。
● すべての元素は、一定の質量を持つ原子からなる。
● 化合物は、異なる種類の元素の原子が簡単な数の比で結合することによってつくられる。
ドルトンは、おのおのの元素に対応する原子が存在すると考え、水素原子の質量を基準にとって1とし、各原子に「相対質量」を割り当てた*。現在の「原子量」の基準は、12Cの原子量を12としているが、基本的にはドルトンの方式である。また、独自の元素記号を考え、化合物の化学式を表現できるようにした。例えば、酸素と炭素の元素記号(それぞれ○と●)を使って、一酸化炭素を
○●、二酸化炭素を○●○と描き表した。これは、今日のCOとCO2に対応している。
---------------------------------------------------------------------------------------------
* 水に対しては、水素と酸素の化合物が、当時水しか知られていなかったため、水は水素と酸素が1原子ずつからできるとした( 「最単純性の原理」を仮定)。その結果、水の構成元素の質量の割合が、水素15%、酸素85%(ラボアジェの研究結果)なので、酸素原子の「相対質量」は 85/15 = 5.66 とした。のちに、より正確な分析値によって7に改めた。今日の酸素の原子量16の約半分の値になったのは、水の組成を水素と酸素が1原子ずつと仮定したためである。
--------------------------------------------------------------------------------------------
ドルトンの原子説を今日的に表現すれば、以下のようになる。
○各々の元素は、固有の原子量を持つ。
○元素Aがm原子、元素Bがn原子からできている化合物は、AmBn(mとnは、簡単な整数)と表される。
このように考えると、当時知られていた「質量保存の法則(化学反応の前後で、物質の総質量は変化しない)」および「定比例の法則(ある一つの化合物の成分元素の質量比は、常に一定である)」を説明することができた。さらに、ドルトン自身が原子説の根拠として「倍数比例の法則(2種の元素A、Bから、2種以上の化合物ができるとき、Aの一定量と化合するBの質量比は簡単な整数となる)」を発表した。
③気体反応の法則(反応体積比の法則)の発見
1808年,ゲイ・リュサック(フランス)が発表した。
●気体反応における気体の体積は、同温・同圧の条件で簡単な整数比になる。
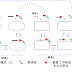
水素と酸素を電気火花で化合させたときの体積比を正確に決めると、水素:酸素=2:1 であった。さらに、窒素と酸素から窒素酸化物ができる反応の結果は、表1のようになり、反応する酸素と窒素の体積は整数比であった。この表にある一酸化窒素ができる反応を例にして以下の説明をする。この反応では、窒素1体積と酸素1体積の反応によって一酸化窒素2体積が生成するので、この反応は図1A のように表される。そうすると、反応の前後で反応系の体積は同じで、粒子の総数が半分になる。言い換えると一酸化窒素は窒素や酸素と同じ粒子数で2倍の体積を持つことになる。ドルトンはそうだと考えた。
 |
図1. 気体反応の法則の一酸化窒素の生成反応への適用。
窒素1体積と酸素1体積の反応によって一酸化窒素2体積が生成する事実を踏まえたドルトン(1A)とアボガドロ(1B)の考え方。
|
④アボガドロの分子説
1811年、アボガドロ(イタリア)が、ドルトンの原子説を修正して気体反応の法則を説明するのに成功した。その時、次の2つの仮定をした。
❶単体の気体では、2 個の原子からなる粒子(分子)が構成単位である。
❷同温、同圧では、同じ体積の気体には、どのような種類の気体でも同数の粒子が含まれる。
図1Bに示すように、①の仮定のように2 個の原子からなる窒素と酸素が体積比1:1で反応すると、一酸化窒素2体積が生成して❷の仮定のように同一体積に同数の粒子が含まれるようになる。
分子説は、当時の化学者にすんなりと受け入れられなかった。容認されたのは、半世紀の後で、アボガドロの死後のことであった。いろいろ要因はあるとされるが、化学界の重鎮ベルセリウス(スウェーデン)の批判もその一つとされる。彼は、ドルトンの原子説の重要性を認め、正しい原子量を得る努力をした。しかし、化合物は原子間の電気的な力で生成されると考え、同種の原子どうしは結合しないと主張した。そして、当時の化学界が分子説を拒絶した結果、物質の化学式の表記が研究者によって異なり、そのため元素の原子量の値が確定しない状態であった。
⑤カールスルーエの国際化学会議
1860年、約120人の化学者が集まり、当時混乱していた原子・分子の概念、元素記号の問題、原子量の決め方などを議論した。そして、原子量は水素原子を基準(原子量 1)にして示すこと、および、元素記号はベルセリウスの記号( 1813年)を用い、ラテン名の最初の1文字または2文字で表す**ことが決議された。
---------------------------------------------------------------------------------------------
** H2Oのように、原子の数を下付きにするのは、リービヒッヒ(ドイツ)が導入(1834年)した。また、反応を等式で示す表現は、1840年代に、グレアム(イギリス)が始めた。
---------------------------------------------------------------------------------------------
この会議でカニッツアロ(イタリア)がアボガドロの分子説を再評価したことが有名で、分子説を原子量・分子量の決定の基準にすべきであると主張した。決議には至らなかったが、参加者に自分の論文を配布し注意を喚起した。このことが契機となり、分子説が化学者の間に広まった。しかし、原子・分子の実在が証明されたのは、20世紀初めことである。
II 原子説・分子説の発展
①気体分子運動論の発展と原子説への攻撃
19世紀後半に、クラウジュウス(ドイツ)、マクスウェル(イギリス)、ボルツマン(ドイツ)らが、気体分子運動論を発展させた。この理論では、圧力や温度などの気体の性質を、多数の気体分子の運動(平均化された)に基づいて説明した。ここでは、初期の理論で解説する。
N個の理想気体分子が体積V の中にあるとする。壁面への分子N個の衝突による圧力(p)は、分子の質量をm、分子の速度を𝒗とすると、次式が得られる。
p =(N/3V)m<𝒗2 >・・・・・・・・・・式1
この式と 𝒑𝑽 = 𝑹𝑻=NA𝒌𝑻 から、気体分子1個当たりの平均運動エネルギーは、
(1/2) m<𝒗2 > =(3/2)kT・・・・・・・・式2
となる。ここで、𝑹は気体定数、𝒌 はボルツマン定数、 NA はアボガドロ定数である。
式2は任意の𝒎の値に対し(つまり気体の種類に関係なく)成り立ち、同温ならm<𝒗2
>は同じなので、式1で同圧、同体積の場合Nが同じになる。
気体分子運動論は原子説・分子説を強く支持するものであったが、19世紀末になっても、マッハやオストワルドのような高名な学者が原子説を攻撃した。
②原子・分子の実在性の証明
1905年、アインシュタインが、ブラウン運動の理論を発表した。彼は、水に浮かんだ微粒子のブラウン運動が、水分子が微粒子にランダムに衝突することによって起きると仮定して、一定時間(t)に起きる微粒子の変位(x)の2乗平均<x2>を表す式を示した。
<x2> =(RT/NA )×(1/3πaη)×t
ここで、 a は粒子の直径、 ηは溶媒の粘性率 である。
この理論の正しさを、ぺラン(フランス)が1908年から1912年にかけて実験をして証明した。顕微鏡下での微粒子の運動の観察結果(図2)から、上の理論式が正しいことが分かり、NAの値として6.88 × 1023が得られた。微粒子の鉛直方向の分布を測定するなど種々のアプローチで得たNAの値は、6.5~ 6.9 × 1023であった。アボガドロの業績にちなんで NA はアボガドロ数と命名された。今日ではNA はアボガドロ定数と呼ばれ、6.02 × 1023mol-1と表される。ぺランの研究によって、原子・分子の存在が広く科学者に信じられるようになった。
 |
図2. ぺランが、顕微鏡下に3個の粒子について30秒ごとの位置を方眼紙に写しとった図。
|
その後、X線結晶構造解析、走査型トンネル顕微鏡、クライオ電子顕微鏡などの技術が発展し、より直接的に原子・分子を実感できるようになった。
③「武谷三段階論」で見た原子・分子をめぐる歴史
「武谷三段階論」は、私が大学生の頃に知った唯物弁証法に基づいた自然の認識についての考え方である。これまでの話をこの考え方に沿って眺めてみようと思う。「武谷三段階論」が、坂田晶一著「科学に新しい風を」(新日本新書)に簡潔に解説されている。
「自然の認識は、現象論―実体論―本質論という三段階の環を画きながら螺旋的に進む弁証法的過程だというのです。最初は個別的事実が記述される段階で、ニュートン力学でいえばティコ・ブラーエまでの段階です。第二は、現象の背後にある実体的構造があばきだされる段階、すなわち特殊の構造をもつ対象が特殊の条件の下に特殊の現象を示すことがのべられるケ
プラー的段階です。そして最後は任意の構造をもつ対象が任意の条件の下にいかなる現象をおこすかを予見しうる段階で、ニュートン的段階ともいえましょう。」
ニュートン力学の確立に適用した場合、ティコ・ブラーエが惑星運行の観測を記録したのが現象論的段階、ケプラーが太陽系に関する法則を見つけたのが実体論的段階、ニュートンが運動の法則を発見したのが本質論的段階ということになる。
原子・分子の認識に至る歴史的な流れに「武谷三段階論」を適用してみると、次のようになると考えられる。ボイル・シャルルの法則や化合物の組成や化学反応に関する法則(質量保存の法則、定比例の法則、倍数比例の法則および気体反応の法則)の発見が現象論的段階、ドルトンの原子説およびアボガドロの分子説の提案が実体論的段階ということができる。上述の初期の気体分子運動論は、気体分子の平均運動エネルギーや平均速度の予見を可能にしたが、任意の構造をもつ対象の振る舞いを予見しうる理論と言うには力不足の感じがする。本質論的段階なら気体のみならず固体の現象の予見が期待される。
●多くの固体単体で、比熱と原子量の積が一定になる。
1
グラムの物質の温度を1 ℃あげるのに必要な熱量が比熱だから、原子量に重さの単位グラムをつけた量(1モル)の熱容量(モル熱容量)が一定ということである(表2)。実は、モル熱容量 =3R (=25 ジュール/ケルビン)であることが、本質論的段階に達すると見えてくる。その段階とはボルツマンやギッブス(アメリカ)が確立・発展させた統計力学で、これによってミクロの立場から様々なマクロの現象の説明が可能になった。
 |
図3. カノニカル分配関数(Z)から熱力学量を導く際の筋道。記号は本文参照。参考資料10にある図。
|
統計力学の教科書の記述に基づいて、この理論によって任意の構造をもつ対象の振る舞いを予見できる様子を見てみたい。田中
一義著「統計力学入門:化学の視点から」(化学同人)に「カノニカル分配関数と熱力学量との関係」の章があって、カノニカル分配関数(Z)から内部エネルギー(U)、エントロピー(S)、ヘルムホルツの自由エネルギー(A)、圧力(p)、ギッブスの自由エネルギー(G)などの熱力学量を導く際の筋道を示すスキーム(図3)がのっている。カノニカル分配関数は、N、VおよびTが一定で熱的平衡状態にある粒子集合全体(系)を扱うときの分配関数である。任意の具体的な系に対しZを計算して上記の熱力学量を導くのを可能にするのが統計力学である。
単原子分子の理想気体の場合、Zを計算するのに、体積Vの中にN個の分子があってTが一定の条件で分子が飛び回っているモデルを考える。そうすると最終的にU =(3/2)NkTが得られる。これは式2をN倍したものに等しい。また、圧力については最終的に、p = NkT/V が得られるので、1モルの気体(N=NA)では、NA𝒌 = R なので𝒑𝑽 = 𝑹𝑻が導かれる。
また、固体単体の原子の場合は、Zを計算するのに、固体をつくっているN個の分子がT一定の条件において、同じ振動数でそれぞれ独立に振動していると考える。この場合には最終的にU
= 3NkTが得られ、固体の量が1モル(N=NA)のときU = 3 𝑹𝑻となる。したがって、固体のモル熱容量(定容)は、Cv = ∂U/∂T= 3 𝑹となる。ちなみに、単原子分子の理想気体のモル熱容量(定容)は、Cv =∂U/∂T= (3/2 )𝑹となる。
III 原子説・分子説のすごさ
運動する粒子と言いう観点から見た原子説・分子説の発展は、上記の通りである。原子説・分子説の発展のもう一つの流れに、化学結合論がある。ベルセリウスは、アボガドロの分子説に対して、同種の原子どうしは結合しないと主張した。この主張はカニッツアロの努力によって退けられ、水素や酸素のような2原子分子が認められるようになった。このような原子間の結合を説明する共有結合の概念が提唱されたのは、1916年のことでルイス(アメリカ)による。それは、オクテット則(結合する各原子が価電子を8個もつ。水素原子は2個)と呼ばれる。1926年には、シュレーディンガーが量子力学の基礎となる方程式を考案した。この式が原子内の電子に適用され、電子雲を使った原子の描像が得られた。オクテット則が成り立つ理由ははっきりしなかったが、1927年にハイトラーとロンドンが量子力学を水素分子に応用し、共有結合の理論的説明に成功した。
このような歴史の流れを見ると、原子説・分子説が統計力学と量子化学の確立に密接に関係していることが分かる。このような事実に基づいてのことと思うが、ノーベル賞学者ファインマンは自らの物理学の教科書の中で、原子説は科学的知識の中で最も大切なものだと指摘している。この指摘に続けて、次のように述べている。
筆者は、現代を代表する大物理学者の深い洞察に感銘を受けた次第である。
「(原子説では、)すべてのものはアトム――永久に動きまわっている小さな粒で、近い距離では互いに引き合うが、あまり近づくと互いに反発する――からできている、というのである。これに少し洞察と思考とを加えるならば、この文の中に、我々の自然界に関して実に厖大な情報量が含まれていることが分かる。」 (下線は筆者による強調)
参考資料
1)廣田 襄著「現代化学史: 原子・分子の科学の発展」京都大学学術出版会、2013年
2)久保昌二著「化学史:化学理論発展の歴史的背景」白水社、1966年
3)竹内敬人著「人物で語る化学入門」岩波書店、2010年
4)竹内敬人著「化学の基本7法則」岩波書店、1998年
5)日本化学会編「化学史・常識を見直す:教科書の誤りはなぜ生まれたか?」講談社、1988年
6)西条敏美著 「物理定数とは何か:自然を支配する普遍数のふしぎ」講談社、1996年
7)石原顕光著「トコトンやさしい元素の本」日刊工業新聞社、2017年
8)井沢省吾著 「トコトンやさしい化学の本」日刊工業新聞社、2014年
9)W.H.ブロック著、大野誠・梅田淳・菊池好行訳「化学の歴史 Ⅰ(科学史ライブラリー)」、朝倉書店、2003年
10)田中一義著「統計力学入門:化学の視点から」化学同人、2014年
11)砂川重信著「エネルギーの物理学:現代物理学入門」河出書房新社、1972年
12)R.P.ファインマン、R. B.レイトン、M. サンズ著, 坪井 忠二訳「ファインマン物理 I 力学」岩波書店、1987年
12)R.P.ファインマン、R. B.レイトン、M. サンズ著, 坪井 忠二訳「ファインマン物理 I 力学」岩波書店、1987年