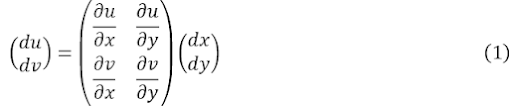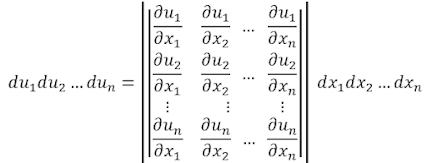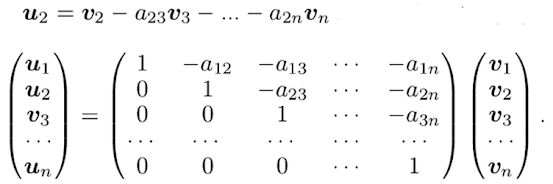十年ほど前のことですが、隠居の暇に飽かせて一念発起し、学生時代(1965年頃)に少しかじったことのある統計力学の勉強を始めしました。手始めに読んだ砂川重信著「エネルギーの物理学」河出書房新社(1972)に、「・・・ このことは、力学のリュービュの定理という法則によって保証されるのだが、これについての議論は省略しよう。 ・・・」とあってこの定理のことが気にかかっていました。今回の記事はリュービュの定理について勉強した結果のまとめです。定理の証明の道筋をたどったうえで、この定義が統計力学の基本原理である等重率の仮定やエルゴード定理とどのように関わるかについても触れます。
N個の粒子からなる系の運動状態は、3N次元の位置座標と3N次元の運動量座標で指定される6N 次元の位相空間(Γ空間)の1点として表わすことができる。この点を「代表点」と呼ぶ。系を構成する粒子の運動に伴って、代表点はΓ空間内を移動する。N個の同様な粒子からなる系が無数にあって、それらの系の代表点を同じΓ空間に一様に分布させたとすると、代表点が密に存在するΓ空間をイメージすることができる。接近した代表点の集団の運動に関して、その集団が存在する領域の体積が移動の前後で変化しないことが知られている。これはリュービュの定理と呼ばれる。今回の記事は、この定理の証明から始め、Γ空間における代表点の密度を定義したうえで、Γ空間の各点で密度が時間変化をしない条件を求めるという流れで進める。
この定理の証明の過程で高次元の座標変換を扱うが、ここでは簡明に2次元での座標変換を理解しておくことにする(参考資料1)。xy-直交座標からuv-座標への座標変数の変換を考える。それぞれの座標変数の間に
で表される関係があって、座標軸の目盛りや方向が変るとする。このような条件の下に、xy-直交座標上の面積素片の面積dxdyが座標変換の後にuv-座標でどう表わされるかを知るのが当面の課題である。
となる。これらの式をベクトルと行列を使って
と書くことができ、xy-座標からuv-座標への座標変換を、局所的には行列
この変換を互いに直行する2本のベクトル
に対して行った結果、それぞれdu、dvになったとすると
このベクトル対の変換を、行列から行列(du dv)への変換として表わすことができる。
 そうすると、(2)は
そうすると、(2)はと変形され、さらに、この式の両辺の行列から行列式を作るととなる。
ここで、この式の図形的な意味を考えてみる。このために、「n個のベクトルで張られるn次元超平行体の体積(2次元では平行四辺形の面積)が、それらのベクトルで構成される行列から作られる行列式の絶対値で表わされる注[i])」という定理を使う。(3)の右辺の行列を構成する2本の列ベクトル
で定まる平行四辺形を考えると、その面積は(4)の右辺の行列式の絶対値で与えられる。よって
となる。この式の右辺に現れる行列式は、座標変換のヤコビアンと称せられ、変換前後の面積素片の面積の比を表す。
----------------------------------------------------------------------------
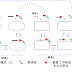
続いて、式(5)の図形的意味を座標変換として考える。図Aで示すように、xy-直交座標上の長方形(レッド)は、座標変数の1次変換によってuv-斜交座標上の平行四辺形(ブルー)に変換される。変換によって座標軸の換わる様子が一目で分かるように、長方形の2辺をxy-直交座標の座標軸に重ねて描いた。次に、uv-斜交座標系の平行四辺形を直交座標系の長方形(グリーン)に、面積を保ったまま変換することを考える(図B)。このような変換をするには、uv-斜交座標の基底ベクトルに対してシュミットの直交化を行なえばよい。これにより斜交座標のv軸は目盛りが変わって、u軸に直交する軸に移る。ここで、
軸を改めてuv-直交座標系のv軸と見なせば、初めのxy-直交座標系が最終的に同一平面上でuv-直交座標系に変換されたことになる。この変換によってxy-直交座標系のdx 、dyが作る微小長方形(図A 、レッド)は、uv-直交座標系のdu、dvが作る微小長方形(図B 、グリーン)に換わり、長方形の面積はそれぞれdxdy、dudvである。ところで、(5)の左辺はuv-斜交座標系の平行四辺形(du、dvで作られる、図A,B、ブルー)の面積を表すが、上記の議論に基づいてuv-直交座標系のdu、dvが作る微小長方形(図B、グリーン)の面積dudvと等しいことになる。よって
これまで2次元の座標変換を考えてきたが、n次元座標の変換に対しても同様のことが成り立つ。もとの直交座標(x1, x2,…,xn)から 新しい座標(u1,
u2,…,un) への変数変換が、連続で微分可能な関数
が導かれる。この式は、右辺右側のn本の直交する列ベクトルで構成された行列が、右辺左側の行列(ヤコビ行列)で変換されるとn次元超平行体の辺のベクトルに換わることを示す。このn次元超平行体の辺のベクトルは、シュミットの直交化によってn次元超直方体に変換されて、(6)に対応する式
が得られる。この式の右辺の行列式は座標変換のヤコビアンと呼ばれ、
と記される。この記号を使えば
である。
ここからいよいよ本論に入る(参考資料2-4)。N個の粒子からなる系の運動状態を表す代表点は、粒子の運動に伴って6N次元のΓ空間内を移動する。ここで、接近した代表点の集団からなる体積素片の運動を考え、時刻tにおける体積素片の中心が微小時間dtの後に移動したとする。この移動によって体積素片が変形するので、時間変化による移動を直交座標系{q1(t),q2(t),……, p3N(t)}から新たな座標系{q1(t+dt),q2(t+dt),……, p3N(t+dt)}への変換と見ることができる。上のパラグラフの議論によって、もとの座標上の微小超直方体(体積素片としての)の体積dq1(t)dq2(t),……, dp3N(t)と、新たな座標上の微小超平行体の体積 dq1(t+dt)dq2(+dt),……, dp3N(+dt)の間に、(6)に対応する
が成り立つ。ここで、Jは座標変換のヤコビアンである。
ところで、Γ空間における代表点の移動はハミルトンの正準方程式に従うので、上記の座標変換においてJ=1となることを導くことができる。簡単のために関数{q1(t),q2(t),……, p3N(t)}を関数{q1,q2,……, p3N}と表し、充分に滑らかな関数とすると、qi(t+dt)をテイラー展開して
と表わせる。座標系{q1(t),q2(t),……, p3N(t)}から座標系{q1(t+dt),q2(t+dt),……, p3N(t+dt)}へ変換するときのヤコビアンは
と表わせる。dtの1次の微小項が出てくるのは、主対角線上のみだから
この式で、位置と運動量が共役関係にある括弧どうしの掛け算は
有限な時間sをn分割するとdt =s/nだから、(9)においてi番目の時刻(s/n)i をt、i +1番目の時刻(s/n)(i +1) をt +dtに対応させると
が成り立つ。上式両辺それぞれをi =0からi =n-1まで掛け合わせると
また、体積素片の境界内の代表点の数も変わらない。体積素片の境界上に代表点が十分密にあれば、境界内にある代表点の軌道が境界上の代表点の軌道を横切ることができないし、境界外の代表点の軌道についても同様である。もし軌道が交差したらその交点を初期条件とする二つの運動が可能になるので、ニュートン力学に反するからである。ここで代表点の密度に注目するため、Γ空間を十分細かい細胞に分けて、代表点を各細胞内の一点の座標(q1, q2, ,…q3N, p1, p2, ,…p3N)(簡単のため以後 (q, p)と略す)で示す。このようにΓ空間を離散化したことにより、代表点の密度をある時点におけるΓ空間の単位体積当たりの代表点の数ρ=ρ(q, p, t)として定義できる。上述のように、体積素片の移動によってその体積もそれに含まれる代表点の数も変わらないので、体積素片内の代表点の密度も不変である。このことが、ある領域に含まれる任意の体積素片について成り立てば、その領域全体についても代表点の密度の不変が成り立ち
となる。Γ空間内の領域は、それを埋め尽くす体積素片の変形に伴って領域全体も変形するが、代表点の密度は流れに乗って移動する点では変わらないこと(密度の保存)になる。このようにリュービュの定理を表現することもある。流れに沿って密度が変わらないのは、非圧縮性の液体が管の中を流れる場合と同じである。
これら二つの統計力学の基本原理がリュービュの定理から導かれるので、これを説明する(参考資料5,6)。さて、任意の領域の各座標点における代表点の密度は、位置座標、運動量座標および時間を決めれば決まる。
ρ=ρ(q,
p, t) .
ρを時間 tで微分すると
よって、(9)により
である。第1項は、Γ空間のある一点(q,p)における代表点の密度の時間変化であり、第2項は、この点を含む領域の微小な移動に伴う領域内の代表点の数密度の時間変化を表す。
ここで、任意の領域の座標点(q,p)における代表点の密度ρが、座標点の示す運動状態のエネルギーEのみの関数ρ=ρ(E(q,p))によって表わせる場合には
よって
E(q,p)=H(q,p)であるから、(12)の右辺の括弧は、ハミルトンの正準方程式により
となるので、(12)の右辺は0であり
ρ=ρ(E(q,p)) (14)
と表わされる場合である。ρは、Eを通してq、pの関数であるので、Γ空間における代表点の密度分布関数ρ(q,p)と見ることができる。
ここで、Γ空間でE=一定の条件を満たす代表点の集合を考える。この条件を満たす点の集合は一般にΓ空間内の超曲面である。(13)と(14)によって、この超曲面上ではどこでも代表点の密度が一定である。このような状況は、まったく同じ孤立系(N、V、Eが一定)が非常に多数あって熱平衡にあり、それらの系の代表点の集合がΓ空間内を運動している場合(つまり、ミクロカノニカル集合の場合)である。ただし、曲面では領域の体積を表現できないのでEに微小な幅δEを持たせる。系の代表点の集合はE(p,q)=E~E+δEの領域にしか存在せず、そこではρ(p,q)=一定(≠0)である。このことは、エネルギーEとE+δEの超曲面で挟まれた領域には代表点が均一に分布することを意味する。代表点は多粒子系の微視的状態に対応するので、代表点が均一に分布するとは、「E(p,q)=E~E+δEの領域では、すべての微視的状態の出現確率は等しい」と言うことである。これは等重率の仮定と呼ばれ、統計力学の基本原理である。
次に、(7)と(8)の関係をカノニカル集合(N、V、Tが一定)に適用する。まったく同じような多粒子系が多数あって、温度Tの外界と平衡にあると考える。そして、それらの系の代表点が6N次元のΓ空間内を運動しているとする。この場合は(14)により、Γ空間における系の代表点の密度ρは、Eを通してq、pの関数として決まる。密度分布関数ρ(q,p)を用いて、ミクロな物理量A(p,q)の平均を位相空間全体にわたって取ると、マクロな物理量が平均値<A>として求まる。式で表せば
参考資料
1.
吉田弘幸 著 「大学1・2年生のためのすぐわかる解析力学」東京図書、2024 pp. 1-23(Chapter
1 数学の準備)
2.
上掲書 pp. 134-152(Chapter 9 ハミルトン形式)
3.
相沢 洋⼆ 著 「キーポイント
熱・統計⼒学」岩波書店、1996 pp.121-140
(ポイント7 分子運動の混沌)
4.
馬場 敬之 著 「統計力学キャンパス・ゼミ(改訂2)」マセマ出版社 2023 pp. 42-55 (リウビルの定理と等確率の原理)
5.
https://ocw.kyoto-u.ac.jp/wp-content/uploads/2010/04/2010_toukeibutsurigaku_2.pdf
冨田博之 『統計物理学』講義ノート2005 年3月4版 pp.18-26 (2章 位相空間)
6.
藤原 邦男 , 兵頭 俊夫 著「熱学入門 マクロからミクロへ」東京大学出版会 1995、
pp. 86-109(第6章 古典統計力学の基礎)
(後記)
予め知人に原稿のレビューを依頼しました。その折のコメントや提案を取り入れて本記事を完成しました。ただし、本文中の図示した個所の座標変換については、お墨付きをもらえていません。脚注i)は知人による論考に基づきまました。
注[i])n次元ベクトル空間において、n個のベクトルによって張られるn次元超平行体の体積は、それらのベクトルで構成される行列の行列式の絶対値になることの証明は以下の通り。
、のn本の線形独立なベクトルを考える。これらn本のベクトルが作るn次元平行体Vの体積を|V|とする。そして、これらのベクトルの成分を並べて次のような行列
を作ると、この行列Vに対して定義される行列式|V|の絶対値||V||が、n次元平行体Vの体積|V|を表すこと、すなわち|V |=||V||を証明しよう。
Hn-1をv 2, v 3,……, v nが張る超平面とすると、v 1はこの面から飛び出ている。Hn-1からv 1の終点に向かいHn-1と直交するベクトルをu1とすると、Hn-1上のv 1の起点からu1の起点に向かうベクトルは、v 1のHn-1への正射影Pn-1 v 1で表される。したがって
v1=Pn-1 v
1+u1 ∴ u1= v 1-Pn-1 v 1 .
Pn-1 v 1はv 2, v 3,……, v nの線形結合
よって
この操作を繰り返して
が得られる。ここで、この式の右辺に対して「行列の積の行列式は各々の行列式の積に等しい」という定理を使うと、右辺左側の行列の行列式は1だから
|U | = |V
| .
よって、これら二つの行列式の絶対値も等しい。
||U ||= ||V ||
[2]
|U | = |V | . [4]
[2]、「3」、「4」から
|V |= ||V || .
証明終わり。