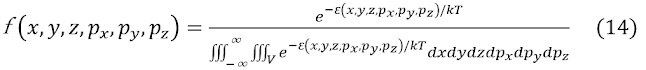気体分子の運動エネルギー分布

 

一般向けのエントロピーの解説本に、気体分子の運動に関して速度分布とエネルギー分布が説明されていましたが、後者の分布について腑に落ちない所があり、改めて勉強しました。この記事はその備忘録です。マクスウェルの速度分布を介さないで、ボルツマン分布からスタートして気体分子の運動エネルギーの分布を導出してみました。初めに分子の一般的な運動についてボルツマン分布を導いたのちに、気体分子の運動量に注目して運動エネルギーの分布を求めるという流れになります。

 

１．ボルツマン分布の導出

N 個の単原子分子からなる理想気体が容器の中で熱平衡の状態にあるとする。このような粒子系の各粒子の運動状態は、3次元の位置座標(x, y, z )上の位置と、3次元の運動量座標(p_x , p_y, p_z)上の運動量により定まるので、6次元の位相空間(μ空間)の一点(x, y, z, p_x , p_y, p_z) で表わされる。容器中の粒子の場合、位置は定まった位置空間Ⅴ内に限られるのに対し、運動量には制約 がなく、3次元の運動量空間のすべての点に及ぶ。 したがって、今後扱う空間は、μ空間の部分領域Vである。我われはμ空間の領域V における粒子の分布を知りたいのであるが、すべての粒子の状態を観測してその分布を知るのは不可能である。しかし、確率論を援用して十分な確度でその分布を知ることができる。

 

V を微小な細胞に分けて、各細胞の体積はすべて同じでɑとする。粒子のエネルギーは粒子の状態を表す6変数の関数ε(x, y, z, p_x , p_y , p_z) であるが、しばらくの間、i番目の細胞内の各粒子のエネルギーをその細胞内の一点で決まるエネルギーの値 ε_iで近似する。N 個の粒子のうちの n_i 個がi番目の細胞に入るような配置{n₁、n_2、……n_i、……}の数は 

                 

である。粒子の総数を 𝑁、粒子のエネルギーの総和を 𝐸とすると

　

である。この条件の下で、Nが大きい（アボガドロ数の程度）と、粒子がエネルギーε_iの細胞に入る確率は、Wに最大値を与える配置{n₁、n_2、……n_i、……}のn_iによって、P_i=n_i/Nとなることが証明されている。そこで、(2)と(3)の条件のもとにWが最大となるn_iを求めるのが課題になる。Wを最大にするのは、logWを最大にするのと同じであることに留意して、(2)と(3)の条件の下で、logWが極値をとる条件を求める。

 

　粒子の分布｛n₁、n_2、……n_i、……｝のn_iにわずかの変化δn_i（i = 1, 2,3,…）を与えた際のlogWの変化を求めるのであるが、その変化δn_iによって(2)と(3)の左辺は変わらないから、

となる。logW すなわち(1)の右辺の自然対数をとると、Starlingの公式により近似的に

となる。n_iにわずかの変化δn_i（i = 1, 2,3,…）を与えた際のlogWの変化は、

となる。logWが極値をとるところでは、δn₁, δn₂, δn₃,.....が条件(4)と(5)を満たして微小なら、δlogW=0であるから

となる。

 

logWが極値をとる条件として、(6)に(4)と(5)の二つの条件が加わると、δn_１,δn_２,δn_３…のうちで独立に変化できる変数が2個減る。扱っている粒子系では、ε_i すべてが等しいということは無いので、ε₁≠ε₂となるように番号をつけることができる。よってδn_１とδn_２をδn₃,δn_4,δn₅,…の従属変数とすると、δn₃,δn_4,δn₅,…は独立に変化することができる。

ここでLagrangeの未定乗数法を適用し、付加条件の式(4)と(5)に値が未定の数－α、－βを掛けて、logWが極値をとる条件の式(6)に加えると

となる。ところで (7)式の i = 1とi = 2の項の括弧が0になるようにαと

βを選んだとすると

である。先に述べたように、ε₁≠ε₂となるように番号を付けたので、この連立方程式は解くことができてαとβが決まる。そうすると、(7)は i = 1, 2 に対して成立する。また、(7)でi ≧ 3のすべての項の和が０になるには、δn_３,δn_４,δn_５,_…が独立に変化するため

でなければならない。よって、(7)は全てのiに対して成り立ち

　　　　　　　　　　

となる。これは、あたかも(7)がδn₁, δn₂, δn₃,δn₄,.....が独立に変化し得るときの極値条件と同じである。(8)を

　　　　　　　
と書き直し、

となるから、この式と（9）から

　　　　　　　　　　　　　

となり、ボルツマン分布の式が得られる。この式のβは、後で求めるように β＝1/kT となるので、熱力学との対応をとって、上式は   

 と表わされる。

２．連続型のボルツマン分布の誘導

 これから、離散的なボルツマン分布の式(11)をμ空間の6次元座標(x, y, z, p_x , p_y, p_z)を使った連続的な分布に変換する。(7)の両辺を細胞の体積ɑ で割ると

　　　　　   

となる。近似的な言い方であるが、細胞が微細な6 次元直方体で、その体積ɑがdxdydzdp_xdp_ydp_z に等しければ、ε_iをε(x, y, z, p_x , p_y , p_z)  に戻して、(12)式右辺の分母の和は、次式左辺のようにμ空間の定義域Vにおける積分で表され、

　                   

となる。右辺内側の積分記号の添え字Vは、μ空間の領域V（太字）の定義に用いた位置空間の領域である。また、(12) の左辺はi番目の細胞内の粒子の平均数密度であるが、細胞が十分に微細な場合、平均密度は細胞内の1点(x, y, z, p_x , p_y , p_z)における粒子の数密度n(x, y, z, p_x , p_y , p_z)に置き換えても誤差は無視できる。以上によって（12）は

　

になる。これは(12)の和を積分に置き換えた近似式であるが、 (12)はエネルギーを離散化して得られた数密度の近似式であり、 (13)はそれを本来の数密度の式に戻したものである。これをμ空間の定義域V で積分すると、粒子の総数N になる。(13) の両辺を粒子の総数N で割れば粒子分布の確率密度関数

が得られる。この関数はN 個の粒子から無作為に選んだ一粒子が点(x, y, z, p_x , p_y , p_z)に存在する確率密度を表す。確率密度関数を定義域で積分すると1 になる。

 

３．気体分子の運動への応用

ここまでは、エネルギーが運動量のみならず位置にも依存する粒子系に適用できるμ空間で議論を展開したが、以降、熱平衡にある理想気体分子の運動について議論する。その場合、確率密度関数は位置座標に依存しないので、ｆ(p_x , p_y , p_z)と書いてよいが、定義域はμ空間の領域である。(14)のε(x, y, z, p_x , p_y , p_z)に理想気体分子の運動エネルギーε= (1/2m)(p_x^２＋p_y^２＋p_z^２）を代入すると、

となるが、右辺分母の被積分関数はx, y, z に依存しないので、この3変数による積分は分離できて、分母は

となる。ただし、|V|は位置空間の体積である。この結果を代入して、(15) は

になる。

 　

　(16) はx, y, zに関して定数なので、V で積分すると両辺にその体積|V|がもたらされるが、右辺では分母の|V| とキャンセルされる。左辺の積分結果は|V|ｆ(p_x , p_y , p_z)でありと定義すると、(16) を積分した結果は

である。この関数は全運動量空間を定義域とする確率密度関数で、定義域で積分すると1 になる。

 

４. 気体分子の運動エネルギー分布

続いて、 (17)を使って気体分子の運動エネルギーの分布を表す式を求める。運動量の大きさp＝(p_x^２＋p_y^２＋p_z^２)^1/2を使って、直交座標を極座標に変換するとd p_x d p_y d p_ｚは p^２sinθdpdθdφとなり、これをθとφについて積分すると４πp^２dpになる。したがって、運動量の大きさの分布を表す式

が得られる。(18) の両辺からdp を外すと、pの確率密度関数　

が得られる。

 

次に、(18) の右辺の変数p を粒子のエネルギーε＝p^２/2mに変換して、εの確率密度関数g(ε) を求める。p=(2mε)^1/2、dp＝(m /2)^1/2ε^₋1/2dεにより、（18）の右辺は

      

に変換され、理想気体分子のエネルギー分布を表す式が得られる。そして、εの確率密度関数は

で、しばしば分布関数とよばれる。かくして、気体分子の運動エネルギーの分布を求めるという本題が達成された。

 

 　初めの方でβを1/kTに置き換えたが、ここでβ=1/kTの証明をする。置き換えをせずに論述を進めれば、(19)は　

となる。粒子1個の平均のエネルギー<ε>は、(20)の左辺にεを掛けて0≦ε＜∞の区間で積分して求められる。

　　

右辺の積分は、部分積分によって

となる。したがって

ところで、（20）は、一つの粒子がε~ε+dεのエネルギーを持つ確率であるから、0≦ε＜∞の区間で積分すれば

である。したがって(21)から

が得られる。一方、気体の分子運動の力学に基づいて、粒子の平均の運動エネルギーは、

と導かれるから

となる。この式は、理想気体の運動以外の一般の場合にも成立することが証明されている（参考資料4、§12恒温槽分布）。

ついでながら、（18）からマクスウェル・ボルツマンの速度分布を導いておく。p = mvで、dp = mdvであるから、pをvに換えると、（18）は

に変換され、マクスウェル・ボルツマンの速度分布が得られる。この分布はマクスウェルにより古典的方法により得られた式と一致する。

 

参考資料

1. 藤原 邦男 , 兵頭 俊夫 著「熱学入門　マクロからミクロへ」東京大学出版会　1995.  pp. 97-107（マクスウェル－ボルツマン分布の導出）, pp. 137-142(正準集団と内部エネルギー)
2. 和達 三樹 著 , ⼗河 清 著 , 出⼝ 哲⽣ 著「ゼロからの熱力学と統計力学」岩波書店2005.　pp. 95-126（第5章　古典統計力学）
3. 竹内 淳 著「高校数学でわかるボルツマンの原理」講談社　2008.　pp. 156-195 (統計力学の世界へ)
4. 戸田 盛和 著 「統計力学概論」朝倉書店1952 .  pp. 32-38 （§11エントロピーと熱力学的重率, §12恒温槽分布）

（追記） 予め知人に原稿のレビューを依頼しました。その折コメントと一緒に送られてきた知人の論考を一部に取り入れて本記事を完成しました。

 無断転載禁止